

摘 要: 采用冪指數描述“三明治”式梯度結構形式, 建立鎳基氧化鋁梯度陶瓷涂層在靜態接觸集中力載荷作用下有限元模型, 分析靜態接觸集中力載荷作用下涂層的Mises應力分布, 以及梯度層的厚度、中間層數及結構形式對涂層的Mises應力分布及較大Mises應力發生位置的影響。結果表明:梯度結構對接觸區Mises應力大小及分布影響不大, 但影響較大Mises應力發生位置;合理的梯度結構能避開較大Mises應力發生在表面強化區及梯度區中, 防止陶瓷涂層在接觸載荷作用下疲勞脫落。制備層狀結構梯度陶瓷涂層時, 采用氧化鋁層厚度20μm、線性梯度層厚度80μm、8層中間層, 可改善Mises應力, 適當避開較大Mises應力發生在梯度區。
金屬陶瓷以其優異的耐磨性能展現出廣闊的工程應用前景, 但由于陶瓷材料脆性制約了其應用。隨著3D打印技術的快速發展, 機械制造轉變為可以運用金屬粉體和塑料等可黏合材料, 通過3D打印制造機械零件, 有人形象將這種制造方式轉變稱為從制造過程做“減法運算”轉變為做“加法運算”的改變。機械制造技術的轉變, 使得根據機械零件應力分布特點、動力學性能、零件功能要求及工況條件要求進行功能區劃分, 各功能區之間設計相應的梯度結構漸變成為可能[1-2]。開展基于機械零件功能區差異進行分區選材的設計理論為具有梯度復合材料/結構機械零件設計提供了指導, 將會很大地促進機械設計學科的發展[3-7]。
本文作者以耐磨損、抗接觸疲勞2個功能區為研究對象, 分析Al2O3-Ni陶瓷金屬梯度結構在接觸應力作用下, 不同梯度結構基體內部Mises應力變化。以減少界面應力突變, 改善Mises應力分布、較大Mises應力不發生在表面強化區并避開梯度區為目標, 探討該工況條件下梯度結構的設計方法。
1 功能區結構設計模型
1.1 功能區結構建模
假定某機械零件表層耐磨性能要求高, 同時承受較大的接觸應力作用, 零件的失效形式為磨損和接觸疲勞失效, 零件劃分為表層耐磨區和內部抗接觸疲勞區, 耐磨區和接觸疲勞區之間采用梯度過渡。采用連續介質鎳-鎳/氧化鋁梯度層-氧化鋁模型描述這結構形式。梯度層是由系列中間層疊加而成“三明治”式結構, 是分配不同的材料屬性結合完好的復合中間層, 材料物理性能為各向同性。采用如圖1所示的剛性小球接觸具有梯度結構圓柱體的彈塑性計算模型, 模型起始處于自由應力狀態, 不考慮溫度對材料屬性的影響。模型中剛性小球直接接觸厚度為δ1的氧化鋁層, 基體厚度為δ3, 基體鎳與氧化鋁層間是厚度為δ2的梯度層。
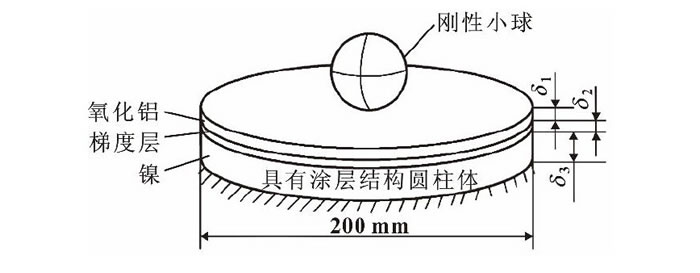
圖1 剛性小球接觸具有梯度涂層結構圓柱體模型
1.2 模型幾何特征和網格劃分
計算模型中的圓柱體總厚度δ1+δ2+δ3=40.4 mm不變, 增加梯度層厚度δ2, 基體厚度δ3相應減少。表1給出了模型參數。靠近鎳基體的梯度層中鎳含量較大, 靠近氧化鋁層的梯度層中氧化鋁含量較大, 梯度層中氧化鋁含量按一定的體積分布函數呈現梯度變化。
表1 模型參數
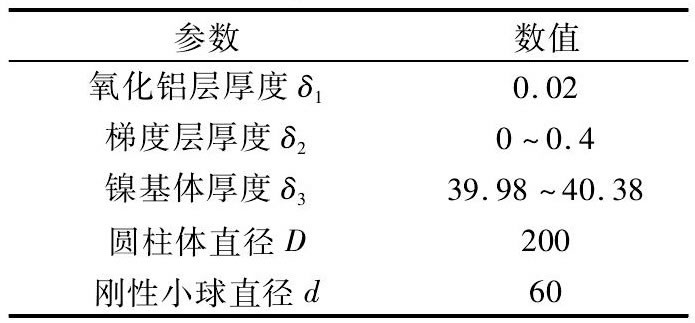
針對模型存在幾何的對稱性, 簡化圖1所示的計算模型, 建立如圖2所示的模型坐標系, 取坐標系所在平面與模型相交所得橫斷面進行分析。在ANSYS中建立圖3所示的二維平面模型, 分析該模型在壓力載荷作用下應力應變, 接觸表面為x軸, 取具有梯度結構圓柱體中心軸為y軸, 初始接觸點為坐標原點O。在小球中心處施加集中力載荷100 N, 并在接觸區域建立赫茲接觸對, 對稱軸y軸上施加對稱約束, 基體底部施加全約束。對靠近接觸面的圓柱體特定區域進行網格細化, 其網格沿著x軸方向劃分50等份, 每份長度40μm, 沿著y軸方向劃分250等份, 每份長度10μm。
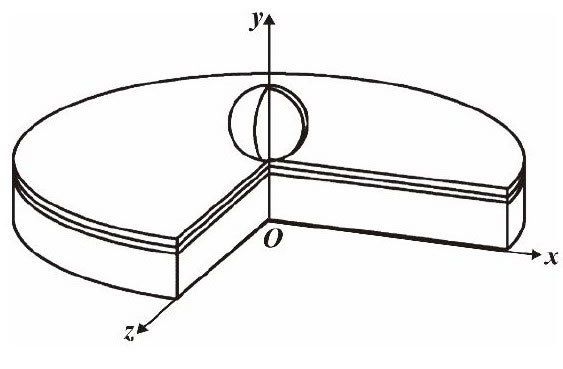
圖2 模型坐標系
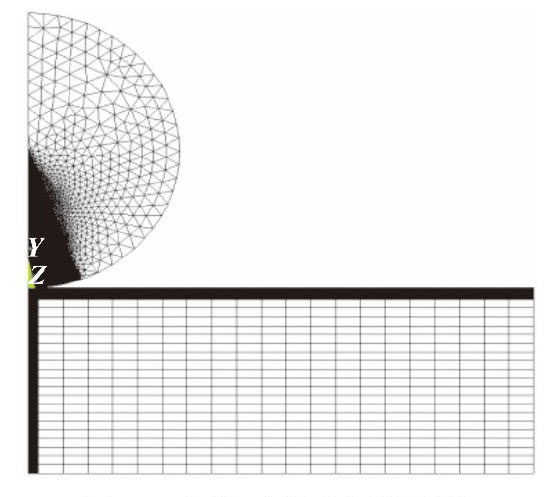
圖3 有限元模型網格劃分
2 Al2O3-Ni二組元梯度材料屬性描述
2.1 梯度層組分分布形式
假定鎳-氧化鋁組成的金屬陶瓷復合材料中的氧化鋁沿梯度層厚度即y軸方向呈現一維連續分布, 氧化鋁的體積分布是y的一元函數。文中氧化鋁分布采用WAKASHIMA等[8]提出的冪函數分布形式, 氧化鋁組元沿厚度方向上體積分布為

式中:Vf (y) 為氧化鋁在梯度層中的體積分數;p為組元成分氧化鋁分布指數;y為沿著Y軸方向梯度層厚度;δ2為梯度層的總厚度。
圖4示出了不同分布指數對應的成分分布曲線。
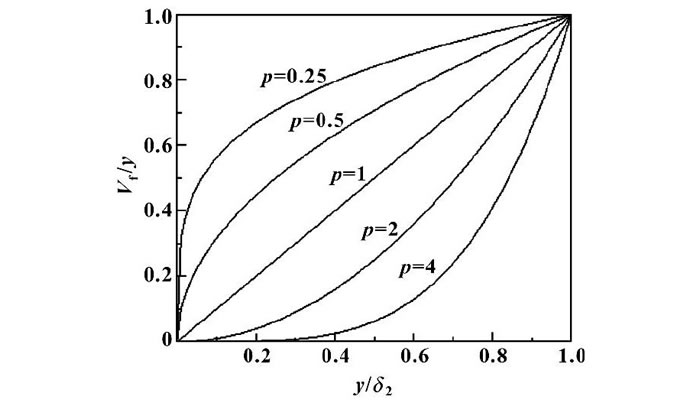
圖4 不同p值下的二組元體積分布曲線
由圖4可知, 通過改變p值的大小, 能得到不同形式漸變梯度層, 就可以改變梯度結構中氧化鋁分布。
2.2 二組元梯度結構分布模型
采用有限元分析梯度層應力應變過程中, 鎳-氧化鋁組成的梯度復合材料考慮為彈性體, 不發生塑性變形, 且計算服從Von Mises屈服條件。梯度層各層材料性能存在微小差別, 各層材料的物理性能同組元的體積分數相關, 按層狀“三明治”結構模擬不同體積分數梯度層[9]。在對梯度復合材料研究中, 較常采用的材料參數計算方法是按TAMURA等[10]提出的修正混合定律計算的。圖5示出了復合材料應力應變關系。梯度中間層材料的應力應變與鎳和氧化鋁的體積分數的關系為

式中:σm、σc分別為鎳和氧化鋁的應力;εm、εc分別為鎳和氧化鋁的應變;σα為復合材料的應力;εα為復合材料的應變;Vm、Vc分別為鎳和氧化鋁的體積分數, Vm+Vc=1;q為應力應變比率, q值按式 (3) 求解, q值取接近二組元材料實驗值4.5 GPa, 關于q的取值可參閱文獻[11]。

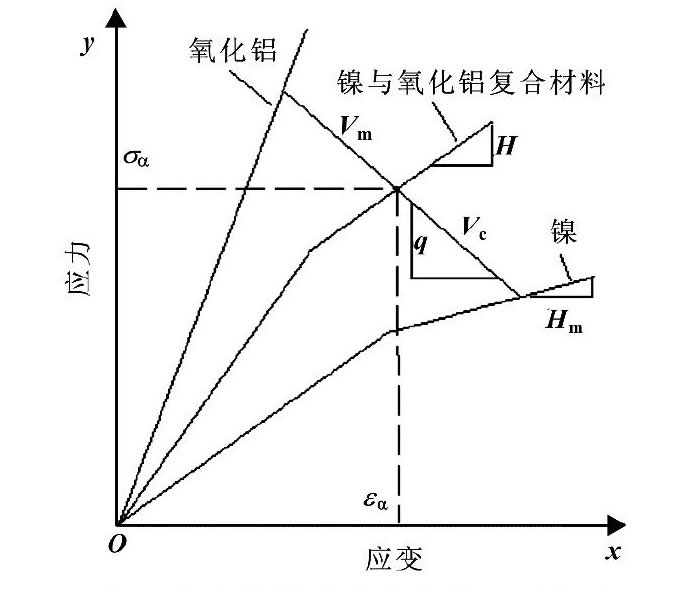
圖5 復合材料應力應變關系示意圖
由式 (2) 、式 (3) 推導出的梯度復合材料的彈性模量為
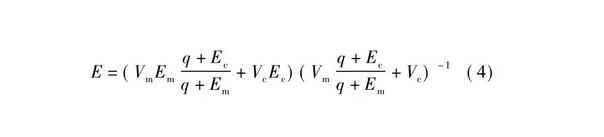
式中:Em、Ec為鎳和氧化鋁的彈性模量。
梯度復合材料切變模量按下式求得[9], 其中Hm為鎳的切變模量。
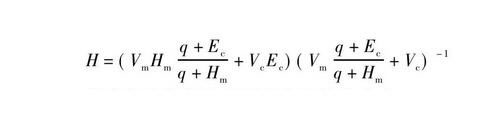
梯度復合材料的屈服強度計算公式為
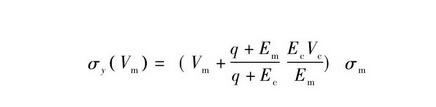
表2給出了剛體小球、鎳基體和氧化鋁材料性能參數。

3 結果與討論
圖6示出了載荷F=100 N作用下無梯度過渡與線性梯度過渡結構模型分析結果對比, 其中氧化鋁層厚度為0.02 mm, 梯度層厚度為0.08 mm。
從圖6 (a) 中可以看出, 增加線性梯度層對接觸區Mises應力分布影響不大, 而較大Mises應力增大了25 MPa, 但增加幅度不很過5%, 較大Mises應力由距接觸表面0.11 mm上升到0.08 mm位置, 進入到了梯度層。
圖6 (b) 表明線性梯度層對接觸區剪應力分布影響也不大, 較大剪應力大小及發生位置發生了變化, 較大剪應力發生位置也由基體位置進入到梯度層中。
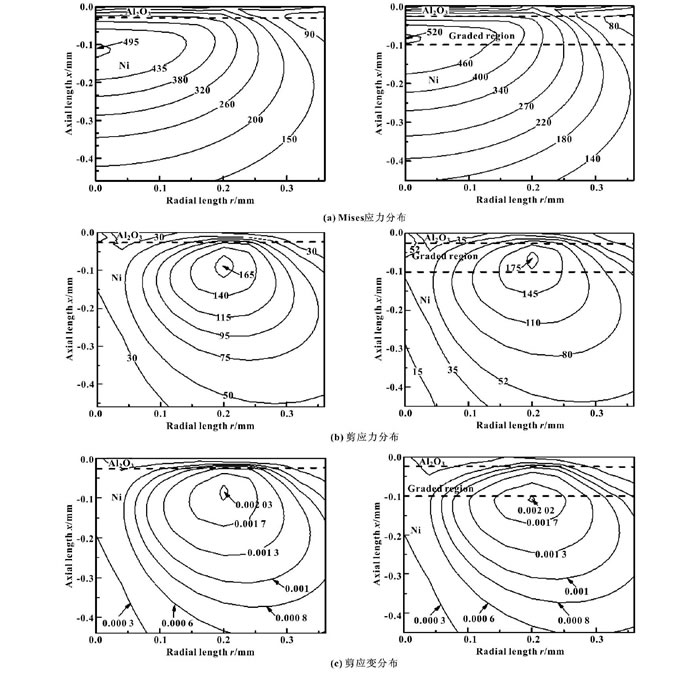
圖6 (c) 表明增加線性梯度結構對剪應變分布形式有所改變, 大小變化不明顯, 較大剪應變發生位置向下移動了。
圖6 無梯度及線性梯度過渡時接觸區Mises應力、剪應力和剪應變分布 (其中δ1=0.02 mm, δ2=0.08 mm)
3.1 梯度結構形式對Mises應力分布的影響
圖7示出了100 N載荷作用下, 氧化鋁層厚度δ1=0.02 mm, 梯度層厚度δ2=0.08 mm, 梯度結構指數與較大Mises應力及較大Mises應力發生位置關系曲線。可以看出, 當梯度結構指數p=0.25時, 接觸區較大Mises應力較大, 且較大Mises應力與接觸表面距離小, 隨著結構指數p的增大, 較大Mises應力逐漸變小, 且發生位置逐漸遠離接觸表面, 靠向基體。當p=4時, 較大Mises應力發生在距接觸表面0.11 mm位置, 已離開了梯度層。而當p=1時, 較大Mises應力發生在距接觸表面0.08 mm位置, 此時接觸區較大Mises應力發生在梯度層內。
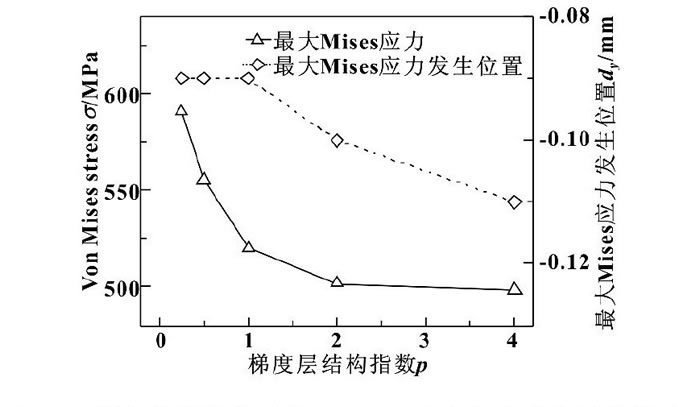
圖7 梯度結構指數對較大Mises應力大小及位置的影響
3.2 梯度層厚度對Mises應力分布的影響
圖8示出了氧化鋁層厚度δ1=0.02 mm, 線性梯度層厚度對較大Mises應力大小及發生位置的影響。可以看出, 在0.08~0.40 mm范圍內, 隨著梯度層厚度增加, 較大Mises應力也隨之增加, 但較大Mises應力增加幅度不大, 較大Mises應力發生位置與接觸表面距離逐漸增大, 但較大Mises應力都發生在梯度層內。梯度層厚度增加, 使得較大Mises應力進入到梯度層中間。
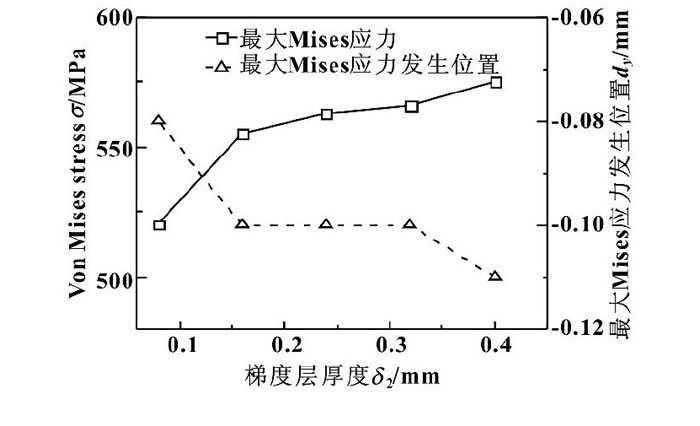
圖8 梯度層厚度對較大Mises應力大小及位置的影響
3.3 梯度層中間層層數對Mises應力分布的影響
圖9示出了氧化鋁層厚度δ1=0.02 mm時, 梯度層厚度δ2=0.24 mm, 線性梯度結構中間層層數對較大Mises應力大小及發生位置的影響。可以看出, 增加梯度層中間層數, 較大Mises應力有所下降, 但中間層數很出8層后, 下降趨勢不明顯, 從梯度層制備工藝考慮, 8層中間層可以獲得較好的性能。梯度層中間層數對較大Mises應力發生位置影響不明顯, 但當中間層達到12層時, 較大Mises應力發生在距表面0.12 mm處, 較8層中間層下移了0.02 mm。
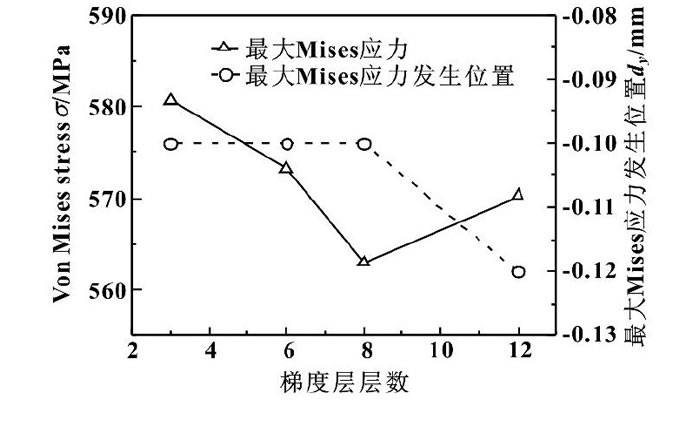
圖9 梯度層層數對較大Mises應力大小及位置的影響
3.4 討論
一般認為在接觸載荷作用下Mises應力是引起接觸區發生接觸疲勞失效的主要誘因, 較大Mises應力很出材料接觸疲勞很限易引起接觸疲勞失效。對于有耐磨損和接觸疲勞要求的零件, 在零件表面制備耐磨層能顯著提高零件的耐磨性能。由于耐磨材料一般屬于脆性材料, 其抗接觸疲勞性能較差, 制備合適的耐磨層厚度才能保證零件足夠的耐磨及抗接觸疲勞性能。過厚的耐磨層和梯度層將會使得較大Mises應力進入梯度層及耐磨層與梯度層層間, 對提高零件的耐疲勞性能不利。從接觸區梯度結構形式對接觸區較大Mises應力和較大Mises應力發生位置影響分析可以看出, 梯度結構對Mises應力大小及分布雖有一定的影響, 但影響幅度不大。但梯度結構能顯著減小耐磨層結合面上的熱應力突變, 采用梯度中間層為8層的線性梯度結構可以獲得較好的特性, 可以有效改善熱應力引起的表面耐磨層的脫落[12]。考慮到一般零件均在熱應力和壓應力綜合作用下工作, 為使較大Mises應力離開耐磨區及梯度層, 理論上應盡可能減少耐磨層和梯度層的厚度, 在文中特定載荷工況下, 當耐磨層δ1=0.02 mm, 梯度層δ2=0.08 mm時, 梯度結構對接觸區Mises應力分布影響較小, 較大Mises應力可以達到基本離開梯度區進入基體。
4 結論
(1) 梯度結構對接觸區Mises應力分布影響不大, 但影響較大Mises應力發生位置, 過厚的梯度層和強化層將導致較大Mises應力發生在梯度區或表面強化區。
(2) 梯度結構指數變化能影響較大Mises應力發生位置。采用冪指數p=4梯度結構能使得較大Mises應力離開梯度區進入基體, 較大Mises應力發生位置與接觸表面距離稍大一些;采用8層梯度中間層結構能降低較大Mises應力。
(3) 為改善梯度結構的抗接觸疲勞性能, 應減小耐磨層和梯度層的厚度, 在文中模型中, 采用0.02mm耐磨層、0.08 mm梯度層厚度、8層中間層的線性梯度結構, 能使得較大Mises應力適當避開梯度區, 從而較好防止表面涂層脫落。
參考文獻
[1]夏軍.梯度功能材料的制備技術與應用前景[J].化工新型材料, 2001, 29 (6) :20-22.XIA J.Manufacture technology and application prospect of gredient function material[J].New Chemical Materials, 2001, 29 (6) :20-22.
[2]程西云, 何俊, 肖舒, 等.梯度結構對氧化鋁陶瓷涂層結合強度及抗沖擊性能影響的試驗研究[J].機械工程學報, 2014, 50 (10) :87-92.CHENG X Y, HE J, XIAO S, et al.Experiment study of influences of gradient structure on the bonding strength and impact resistance of Al2O3ceramic coatings[J].Journal of Mechanical Engineering, 2014, 50 (10) :87-92.
[3]YU H T, MU R D, XIE M, et al.Evolution status and processing technologies of thermal barrier coatings[J].Chinese Rare Earths, 2010, 31 (5) :83-87.
[4]LANDAU L D, LIFSCHITZ E M.Theory of elasticity (theoretical physics) [M].3rd ed.Oxford:Butterworth-Heinemann, 1999:8-9.
[5]瓦倫丁L波夫波.接觸力學與摩擦學的原理及其應用[M].北京:清華大學出版社, 2011:44-52.
[6]NA K S, KIM J H.Three-dimensional thermomechanical buckling analysis for functionally graded composite plates[J].Composite Structures, 2006, 73 (4) :413-422.
[7]MARKWORTH A J, SAUNDERS J H.A model of structure optimization for a functionally graded material[J].Materials Letters, 1995, 22 (1) :103-107.
[8]WAKASHIMA K, HIRANO T, NINO M.Space application of advance structure materials[R].Paris:European Space Agency, 1990.
[9]楊曉東, 董澤民, 楊坤, 等.顆粒增強復合材料彈性結構的雙尺度有限元分析[J].機械工程學報, 2012, 48 (8) :34-38.YANG X D, DONG Z M, YANG K, et al.Two scale analysis of elastic structures of particle reinforced composite materials with finite ement method[J].Journal of Mechanical Engineering, 2012, 48 (8) :34-38.
[10]TAMURA I, TOMOTA Y, OZAWA M.Strength and ductility of Fe-Ni-C alloys composed of austenite and martensite with various strength[C]//Proceedings of 3rd International Conference on Strength of Metals and Alloys.Cambridge:Institute of Metals, 1973:611-615.
[11]WILLIAMSON R L, RABIN B H, DRAKE J T.Finite element analysis of thermal residual stress at graded ceramic-metal interface.Part I:Model description and geometrical effect[J].Journal of Applied Physic, 1993, 74 (2) :1310-1320.
[12]程西云, 張政科.梯度結構對氧化鋁/鎳梯度涂層抗熱應力的影響[J].潤滑與密封, 2016, 41 (10) :13-18.CHENG X Y, ZHANG Z K.Influences of gradient structure on thermal shear stresses of Al2O3/Ni gradient coatings[J].Lubrication Engineering, 2016, 41 (10) :13-18.
作者簡介:張政科 (1992—) , 男, 碩士研究生, 研究方向為機械設計及理論.E-mail:1592339735@qq.com.
作者簡介:程西云 (1966—) , 男, 博士, 教授, 研究方向為金屬材料表面改性及機電控制.E-mail:xycheng@stu.edu.cn.