

摘 要: 基于修正的Johnson-Cook本構模型, 在DEFORM中進行氧化鋁陶瓷的切削仿真, 分析了切削速度、切削深度及切削路程對刀具磨損量的影響。研究結果表明, 刀具的較大磨損深度隨切削速度的增大而減小、隨切削深度的增加而增加。磨損深度隨切削路程變化的仿真結果表明, 切削過程中的刀具磨損可分為3個階段, 即初期磨損階段, 正常磨損階段及急劇磨損階段。
0 引言
陶瓷材料具有機械強度高、硬度高, 耐高溫、耐磨、耐腐蝕等優點, 可用于制作切削刀具, 同時在電子、電力、航天航空方面也得到了廣泛的應用。
氧化鋁陶瓷屬于陶瓷材料的一種, 它具有硬脆性、剛性差等特點, 相對于普通的彈塑性材料, 其加工過程不可控制, 加工難度大、精度差, 且在加工時存在邊緣易崩裂, 刀具易磨損等現象。目前, 制約工程陶瓷廣泛應用較重要的因素就是其加工成本高, 加工效率低。據資料統計, 工程陶瓷的加工成本能占到總成本的50%以上, 甚至高達90%。探究車削陶瓷的刀具磨損規律, 并以此為基礎選擇合理的加工參數, 對提高加工效率、減少加工成本、提高加工質量具有重要意義[1-3]。李迎杰等通過金剛石刀具切削加工Si N4基工程陶瓷實驗發現切削速度對切削力、已加工表面粗糙度、刀具耐用度、切削路程等方面有很大的影響[4];薛建勛采用有限元方法, 對不同切削條件下的氧化鋯陶瓷切削加工過程進行仿真, 分析其切削機理、優化加工工藝參數、提高加工質量[5]。基于DEFORM有限元仿真軟件, 并采用修正的Johnson-Cook本構模型, 研究氧化鋁陶瓷車削過程中刀具磨損量與切削速度、切削深度及切削路徑的關系。
1 有限元仿真模型
1.1 工程陶瓷材料本構模型
本構模型描述了材料的應力應變關系, 其合理選取對于仿真結構的正確性具有重要意義[6]。在使用有限元方法研究塑性材料切削過程時, 一般使用Johson-Cook本構模型, 如式 (1) 所示。但此模型主要用于模擬高應變率下的金屬材料, 由于斷裂機理的差異, 該模型對脆性材料并不適用。在陶瓷、混凝土等脆性材料相關的仿真計算中, 主要使用JH-Ⅱ本構模型。相比于Johson-Cook模型, JH-Ⅱ模型增加了材料損傷累計功能, 使得材料的強度隨著損傷演化的累積而逐漸降低, 并將強度模型由分段級形改為連續形。
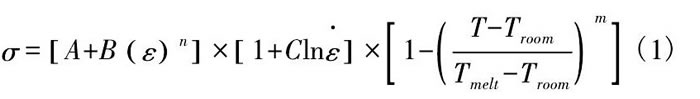
其中:A為屈服應力強度;B為應變強化常數;n為應變強化常數;C為應變率強化參數;m為溫度應變率靈敏度;ε為等效塑性應變;Tmelt為材料熔點溫度;Troom為室溫;為參考應變速率。
在Deform中無適用于脆性材料的本構模型, 但通過改進Johson-Cook模型可得到JH-Ⅱ模型, 在JohnsonCook模型基礎上加入強度的連續性損傷劣化效應, 得到模型如式 (2) 。
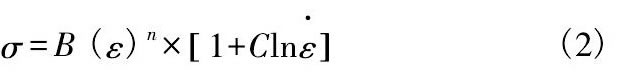
在DEFORM中通過改進Johnson-Cook模型得到JH-Ⅱ模型, 并將其作為有限元中陶瓷材料的本構模型[7]。
1.2 刀具磨損量模型
在車削氧化鋁陶瓷仿真中, 采用能量法、有限差分法分析刀具磨損量。其數學模型如式 (3) 。

其中w為磨損深度;p為接觸壓力;v為滑移速度;T為接觸面溫度;dt為時間增量;a、b為特征常數。
2 DEFORM有限元仿真
在Solidworks內建立工件、刀具的三維幾何模型, 之后將其導入Deform并裝配, 如圖1所示。為減少無關計算量, 將工件簡化為內徑30 mm、外徑32 mm的圓環;刀具按照實際形狀特征建模, 并使刀具繞著圓環轉動以切除工件材料。工件材料為氧化鋁陶瓷, 其楊氏模量為400 GPa, 泊松比為0.233, 熱膨脹系數為7.2×10m/K, 熱導率為35 W (m·K) , 比熱容為0.925 J/ (kg·K) ;刀具材料為金剛石。

圖1 圖形建模
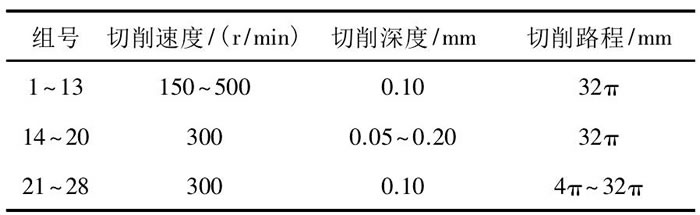
有限元仿真工藝參數設置如表1所示。
表1 單因素實驗表
3 結果與討論
3.1 刀具磨損及切削成屑過程
氧化鋁陶瓷車削過程如圖2所示。在車削仿真中, 刀具與工件表層材料相接觸, 材料受到刀具的擠壓作用, 在二者接觸區域及其附近形成一個應力場, 單元節點受力產生位移, 有限單元產生應力應變變化, 如圖2 (a) 所示。隨著刀具的不斷切入, 材料受到進一步擠壓, 網格過度變形發生失效并飛離工件表面。與塑性材料切削形成連續切屑不同, 陶瓷材料具有硬脆性, 因此陶瓷材料切削時形成崩碎狀粉末, 并在已加工表面產生大小不一的破碎切除, 如圖2 (b) 。圖3所示為刀具磨損狀態有限元仿真結果, 在開始階段刀尖處磨損分布較為均勻, 由磨損中心逐漸向四周均勻擴展延伸, 如圖3 (a) 。隨著切削過程的進行, 磨損不斷增加, 磨損中心向切削刃移動, 磨損分布發生偏移, 由月牙洼逐漸向切削刃延伸, 且磨損程度不斷加劇, 如圖3 (b) 。
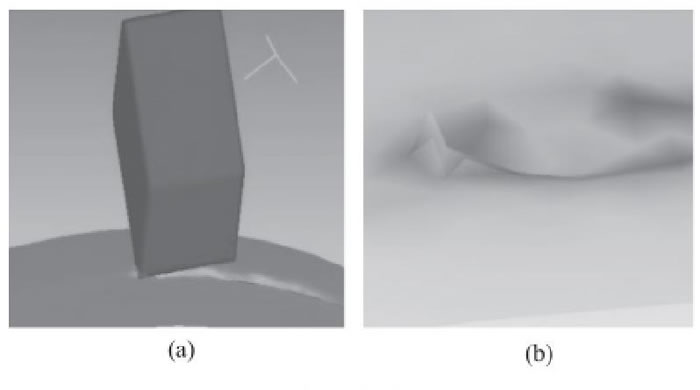
圖2 氧化鋁陶瓷成屑過程
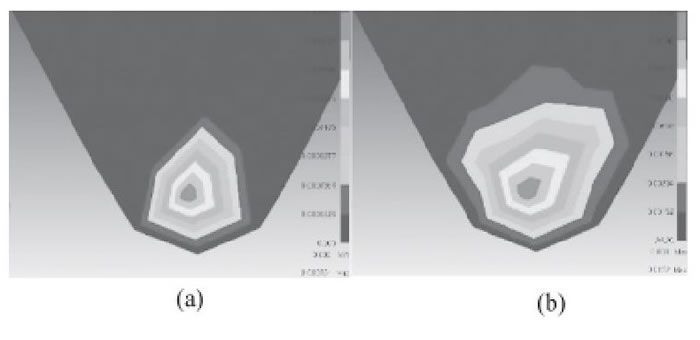
圖3 刀具磨損狀態
3.2 刀具磨損量與切削速度
較大磨損深度與切削速度的關系如圖4所示。在切削深度為0.1 mm, 切削路程為100 mm時, 隨著切削速度由150 r/min逐漸增加至500 r/min, 刀具較大磨損深度呈現逐漸減小的趨勢, 由0.059 3 mm減小到0.036 8 mm。但在減小的過程中, 較大磨損深度數值存在大小不等的波動, 波動的幅度隨著切削速度的增加逐漸減小。當切削速度為150 r/min時, 較大磨損深度的數值較大, 為0.059 3mm, 當速度逐漸增加至375 r/min, 較大磨損深度逐漸減小至較小值, 為0.025 1 mm。
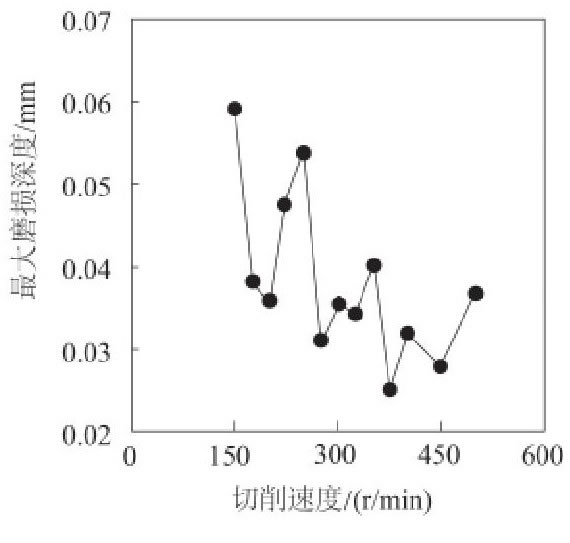
圖4 磨損量與切削速度的關系
3.3 刀具磨損量與切削深度
較大磨損深度與切削深度的關系如圖5所示。當切削速度為300 r/min, 切削路程為100 mm時, 隨著切削深度由0.05 mm逐漸增加至0.2 mm, 刀具較大磨損深度有逐漸增大的趨勢, 由0.036 9 mm增加到0.052 7 mm。切削深度對較大磨損深度的影響程度小于切削速度。當切削深度在0.1 mm~0.15 mm之間時, 磨損深度變化幅度較大, 先快速上升到0.050 7 mm之后又快速下降到0.035 7 mm。當切削深度為0.2 mm時, 較大磨損深度較大, 為0.052 7mm;當切削深度為0.08 mm時, 較大磨損深度較小, 為0.032 8 mm。
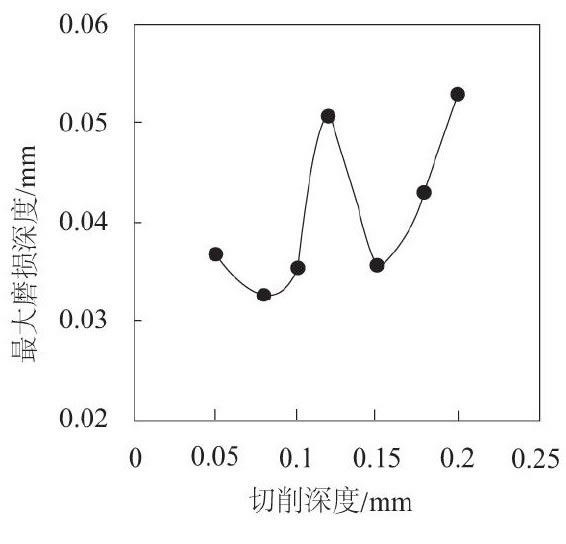
圖5 磨損量與切削深度的關系
3.4 刀具磨損量與切削路程
較大磨損深度與切削路程的關系如圖6所示。在切削速度為300 r/min, 切削深度為0.1 mm的條件下, 當切削路徑的長度由12.5 mm逐漸增加到100 mm的過程中, 刀具的磨損深度隨著切削路程的增加呈現出逐漸增大的趨勢。在切削的初始磨損階段, 切削刃鋒利, 刀具與工件接觸面積小使得接觸應力大, 較大磨損深度隨切削路程長度的增加以一定的速度增加, 切削長度由12.5 mm逐漸增加到37.5 mm時, 磨損深度由0.007 7 mm增加到0.015 6 mm。之后進入穩定磨損階段, 刀具的初期磨損令兩者接觸面積增加, 較小的接觸應力使得此階段內的磨損速度小于初始階段, 切削長度由37.5 mm逐漸增加到75 mm時, 磨損深度由0.015 6 mm增加到0.017 5 mm。較后進入急劇磨損階段, 切削過程中的切削力和切削溫度都大幅增加。當切削長度>75 mm時, 磨損速度急劇增加, 甚至大于初期磨損階段。當切削長度為100 mm時, 較大磨損深度增加至0.035 6 mm。
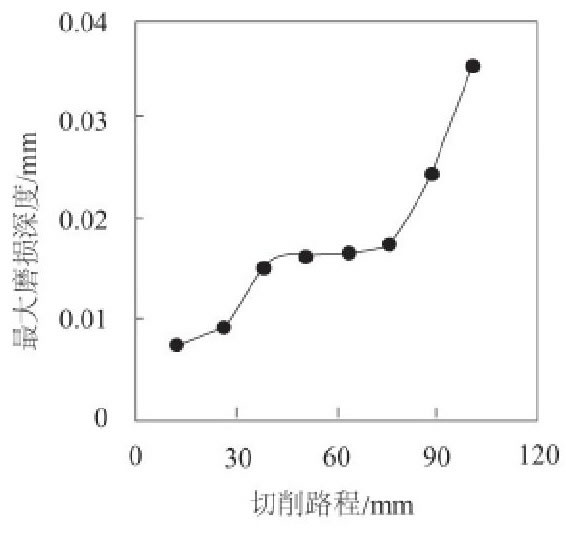
圖6 磨損量與切削路程的關系
4 結語
1) 切削初始階段時, 刀具磨損均勻分布, 隨著切削過程進行, 刀尖磨損從月牙洼處逐步向切削刃處延伸。
2) 單因素仿真實驗結果表明, 較大磨損深度隨著切削速度的增加有減少的趨勢, 隨著切削深度的增加有增加的趨勢。
3) 刀具磨損過程可分為3個階段:開始磨損階段、正常磨損階段、急劇磨損階段。
參考文獻
[1]馬廉潔, 于愛兵, 韓廷水, 等.氟金云母陶瓷車削參數對刀具磨損的影響[J].兵器材料科學工程, 2007, 30 (1) :1-4.
[2]朱志斌, 郭志軍, 劉英, 等.氧化鋁陶瓷的發展與應用[J].陶瓷, 2003 (1) :5-7.
[3]于愛兵, 馬廉潔, 劉家臣, 等.可加工陶瓷材料Zr O2/Ce PO4鉆削刀具的磨損[J].天津大學學報, 2005, 38 (8) :670-673.
[4]李迎杰, 張弘韜, 李享德.PCD刀具切削加工氮化硅 (Si3N4) 基工程陶瓷的合理切削速度[J].金剛石與磨料磨具工程, 1996 (6) :18-20.
[5]薛建勛, 孫全平.氧化鋯陶瓷切削加工有限元仿真分析[J].中國陶瓷, 2012 (10) :28-29, 80.
[6]A.Attanasio, E.Ceretti, S.Rizzuti.3D finite element analysis of tool wear in machining[J].Manufacturing Technology, 2008, 57:61-64.
[7]馬廉潔, 李琛, 曹小兵, 等.基于GA和DEFORM的陶瓷材料切削力數值模擬[J].東北大學學報 (自然科學版) , 2014, 35 (12) :1774-1777.